Problems of the Week – June 25 to June 29

Click here ^[1] for the Problem Extension Worksheet version of the Problems of the Week.
Click here ^[2] for an MS Word version of the Problems of the Week.
The Canadian POTWs are now available here ^[3] for the Extension Worksheet and here ^[4] for the MS Word version.

^[5]Lower Elementary:
Question: What are the next 4 numbers in the pattern below?

50, 45, 46, 41, 42, _____, _____, _____, _____

Answer: 37, 38, 33, 34
Solution: There are two steps in the pattern. To get from 50 to 45, we subtract 5. To get from 45 to 46, we add 1. Then the pattern repeats:

46 – 5 = 41
41 + 1 = 42
42 – 5 = 37
37 + 1 = 38
38 – 5 = 33
33 + 1 = 34

^[6]Upper Elementary:
Question: Chloe gets on her bike at home and rides 2 miles north to the post office. From there, she rides 3 miles west to the library. Then, she rides 4 miles south to the park, then 5 miles east to the farmer’s market. Finally, Chloe rides her bike 2 miles north to her friend Daniel’s house. How far away is Daniel’s house from Chloe’s house? In what direction?
Answer: 2 miles east
Solution: Instead of solving this mentally, students can use a coordinate plane and put Chloe’s house on the origin. The post office is at (0, 2). The library is at (–3, 2). The park is at (–3, –2). The farmer’s market is at (2, –2). Finally, Daniel’s house is at (2, 0), which is 2 miles to the right, or east, of Chloe’s house.

^[7]Middle School:
Question: The figure below is horizontally and vertically symmetrical. What is its area?
(The figure is not drawn to scale.)
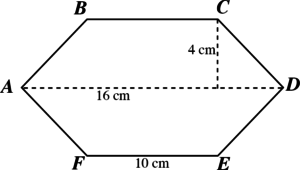^[8]
Answer: 104 square centimeters
Solution: One way we can find the area of the shape by thinking of it as two identical trapezoids. The area of a trapezoid is the average of its two bases multiplied by its height. The bases are 16 cm and 10 cm, so the average is 13 cm. The height is 4 cm. So, the area of one of the trapezoids is 13 × 4 = 52 square centimeters. The area of the whole figure is therefore 52 × 2 = 104 square centimeters.

^[9]Algebra and Up:
Question: There are two perpendicular lines graphed on a plane. Line A goes through the points (2, 1) and (6, 3). Line B goes through (2, 1) and (x, 5). Solve for x.
Answer: x = 0
Solution: To solve for x, we need to know the slope of Line B. Line A and Line B are perpendicular, so the slope of Line B is the opposite of the reciprocal of the slope of Line A. Line A’s slope is ½, so the slope of Line B must be –2. Now that we have a point on the line and its slope, we can write an equation in slope-intercept form:

y = –2x + b
y = 1 x = 2
1 = –4 + b
b = 5
y = –2x + 5
5 is the y–intercept. When y = 5, then x = 0.